Specifications for MSE Trials for North Atlantic Albacore

1 Introduction

The North Atlantic Albacore (NALB) fishery, under the management of the International Commission for the Conservation of Atlantic Tuna (ICCAT), is undergoing a management strategy evaluation (MSE) process.

Management strategy evaluation

Process used in fisheries management to simulate and assess the performance of different management strategies under varying conditions and uncertainties (Figure 1).

There are three main components in an MSE process:

  • Operating models (OMs): a collection of mathematical/statistical models that describe alternative hypotheses of the historical fishery dynamics and specifications for simulating the collection of data and implementation of management measures in the future;
  • Candidate management procedures (CMPs): a set of proposed algorithms that generate management recommendations from fishery data and will be evaluated in the MSE;
  • Performance metrics (PMs): statistics used to quantitatively evaluate the CMPs against specified management objectives.

The OMs, CMPs, and PMs are developed as a collaborative effort between scientists, decision-makers, and other stakeholders in the fishery.

flowchart LR
    subgraph B1["Operating model"]
        direction TB
        i1["Biological and <br> fishery model"]
        f1["Data generation"]
    end

    subgraph B2["Management procedure"]
        direction BT
        i2["Estimation method"] 
        f2["Harvest control rule"]
    end
    f1 --> i2
    f2 --Implementation--> i1
    i1 --> f1
    i2 --> f2
    B1 --> i3["Performance metrics"]
    style B1 fill:#d4f5ba
    style B2 fill:#b9c8fc
    style i3 fill:#fcf7b9
    style i1 fill:#ffffff
    style f1 fill:#ffffff
    style i2 fill:#ffffff
    style f2 fill:#ffffff
    
    %% Set all nodes to black text
    linkStyle default color:#000000
    classDef blackText color:#000000;
    class i1,f1,i2,f2,i3,B1,B2 blackText;
Figure 1: Management strategy evaluation (MSE) framework.

1.1 About this document

This document describes the specifications for the OMs, CMPs, and PMs that have been proposed and developed for the NALB fishery. It is a living document and will be continued to be updated so that it reflects the current state of the NALB MSE process. Members of the Albacore Species Group (ALBSG) are encouraged to provide feedback, comments, or edits to any part of this document.

The document is written using the Quarto format and can edited in any text editor. The source document is available on the MSE GitHub repository. ALBSG members can make edits to the document either directly in the online repository or by cloning the repository and submitting pull requests with their edits. Alternatively, they can email questions or comments to Agurtzane Urtizberea. The former approach has the advantage that all comments, questions, and edits are immediately visible to all members of the ALBSG. The Discussions feature on the Github repository can also be used to post questions, comments, or points for discussion related to any aspect of this document or the MSE process in general.

This document is available at the NALB MSE homepage.

2 MSE framework

The R software has been used to developed the MSE code for the NABL fishery. All code is open-source and can be found on the MSE GitHub repository.

The code developed for the NALB MSE uses the FLBEIA framework. FLBEIA (Garcia et al., 2017) is an R package that has been developed for conducting bio-economic evaluation of fisheries management strategies. The software allows the bio-economic evaluation of a wide range of management strategies in a great variety of case studies such as multi-stock, multi-fleet, stochastic and seasonal configurations. FLBEIA is built using FLR libraries. FLR is a collaborative project oriented to develop quantitative fisheries management tools.

3 Stock assessment

Previously, the NALB OMs were based on the 2013 stock assessment (Merino et al., 2020, 2014) using the MULTIFAN-CL platform (Fournier et al., 1998).

A new stock assessment was conducted in 2023 (ICCAT, 2023) using the Stock Synthesis (SS3) platform (Methot and Wetzel, 2013). The NALB OMs have been updated based on this new assessment.

The data used in the 2023 NALB assessment as well as the structure and assumptions of the assessment model are summarized in the sections below.

Table 1: Fishing fleets included the 2023 NALB stock assessment. The last column indicates if the fleet had an associated index of abundance (catch-per-unit-effort, CPUE).
Fleet code Description CPUE included?
1_BB Baitboat (Spain, France) Yes
2_BB_isl Baitboat islands (Portugal Madeira/Azores, Spain Canary) for quarters 1, 3, and 4 No
3_TR_GN Troll (Spain, France) and Gillnets (France, Ireland) No
4_MWT Mid-water trawl (France, Ireland) No
5_JPLL_N Japan longline north 30 Yes
6_JPLL_S Japan longline south 30 Yes
7_TAILL_N Taiwan longline north 30 Yes
8_TAILL_S Taiwan longline south 30 Yes
9_USLL_N US and Canada longline north 30 Yes
10_USLL_S US longline south 30 Yes
11_VENLL Venezuela longline Yes
12_MIX_KR_PA Mixed flags longline (KR, PA, CHN) No
13_OthLL Other longline No
14_OthSurf Other surface gears No
15_BBisl_s2 Baitboat islands (Portugal Madeira/Azores, Spain Canary) for quarter 2 No

3.1 Data

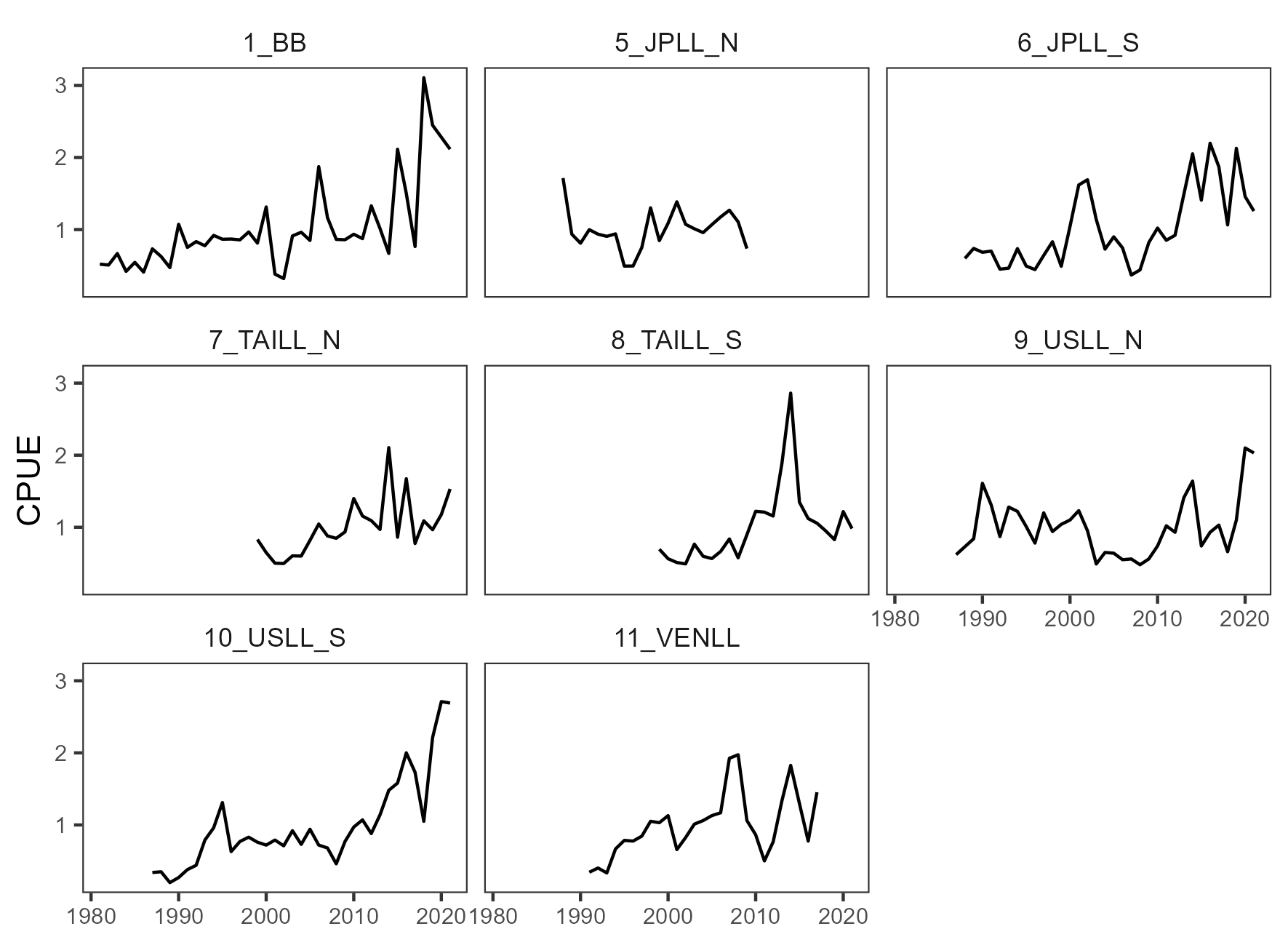
The period covered was from 1930 to 2021. The assessment mainly used landings data from longline (LL) and baitboat (BB) fleets, with a total of 15 fleets included in the model (Table 1 and Figure 2). There were seven LL and one BB (Spain and France) catch-per-unit-effort (CPUE) indices (Figure 3). The catchability coefficients for the CPUE indices were assumed to be time-invariant.

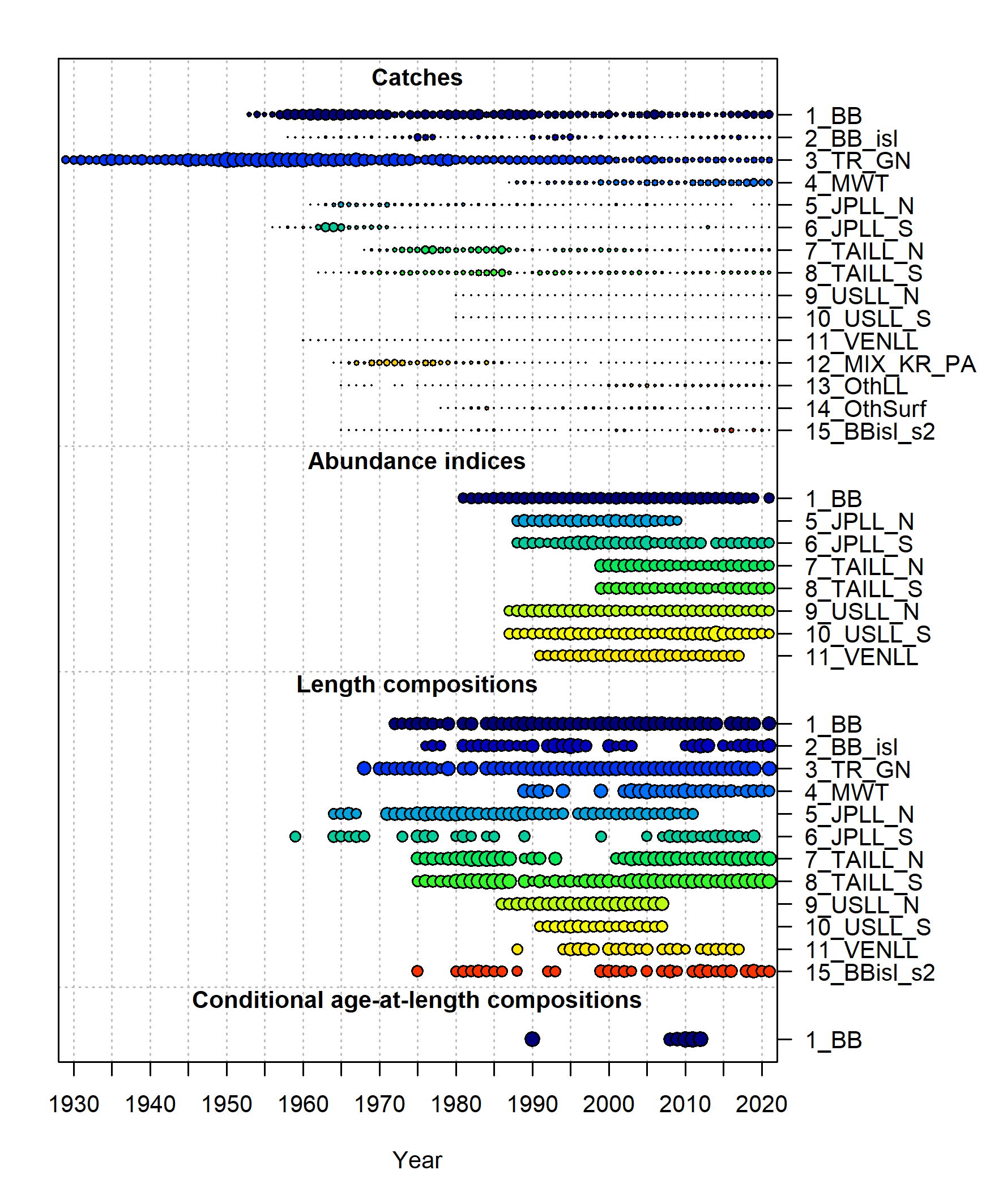
Figure 2: Summary of the data used in the 2023 NALB stock assessment. The bubble size represents the quantity or precision of the data.

Length composition data from 12 fleets were included in the model, mostly from LL and BB fleets and for the period after 1970 (Figure 2). The effective sample size (ESS) for the length composition data was established by adjusting ESS until unity was reached between modeled ESS and the Francis suggested sample size (Francis, 2011). Conditional age-at-length (CAAL) data was also included for the BB (France and Spain) fleet.

Figure 3: Indices of abundance (CPUE) by fleet included in the NALB assessment model.

3.2 Model structure

The model was configured yearly (one season per year), one sex, one area, and a total of 16 age groups (0 to 15+). The spawning timing was January 1st.

3.3 Biological Parameters

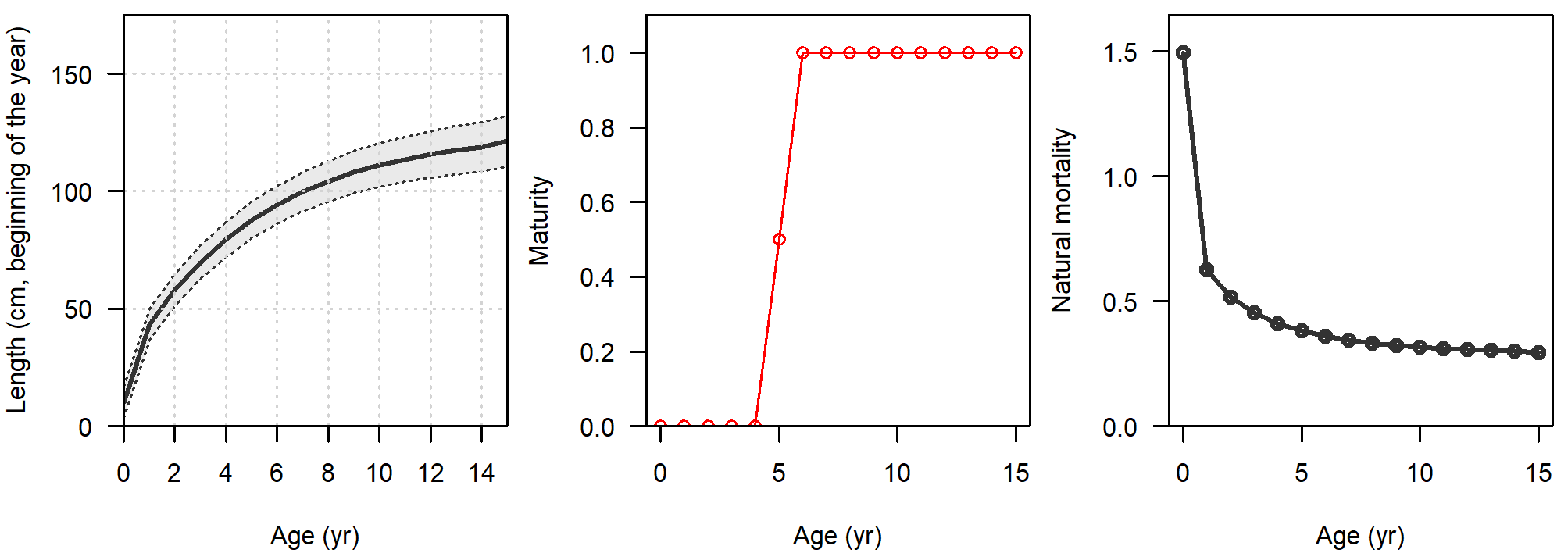
Natural mortality (M) was age-specific and parametrized following Lorenzen (1996), with a reference M equal to 0.36 for age 6 based on the assumption of a maximum age of 15 years (Hamel and Cope, 2022). Maturity-at-age was knife-edge, with 50% at age-5 and 100% thereafter. Fecundity was proportional to body weight. Growth was parametrized following the von Bertalanffy curve (Schnute, 1981) and parameters were estimated within the model. Variability of lengths-at-age was assumed to be a function of age. Figure 4 shows a summary of the biological parametrization.

Figure 4: Growth, maturity, and natural mortality parametrized in the NALB assessment model.

3.4 Stock-Recruitment

Expected recruitment to age-0 was calculated from the total spawning stock biomass using the Beverton-Holt stock-recruit function. Recruitment settlement was assumed to occur at month 6. The standard error for the log-normally distributed recruitment deviations (sigmaR) was fixed to 0.4. Steepness (h) was estimated within the model with a prior of 0.75 taken from the 2013 assessment.

3.5 Selectivity

Selectivity was modelled as a function of length. Dome-shaped selectivity was allowed for several LL and BB fleets, while an asymptotic selectivity was speficied for the US and Venezuela LL fleets. Splines were also used for the BB (Spain and France) and mid-water trawl. Time blocks were specified for some fleets due to changes in length composition data.

4 Operating Models

4.1 Reference OMs

During 2023 and 2024, the ALBSG developed a set of OMs considering variations in natural mortality (M), variability in recruitment (sigmaR), and the weighting of the following data sources:

  • Base case (no change)
  • Upweight (\(\lambda=2\)) CPUE data
  • Upweight (\(\lambda=2\)) size (i.e., length composition) data
  • Upweight (\(\lambda=2\)) age (i.e., CAAL) data

Per weighting scenario, 400 models were run in SS3 by randomly varying the M and sigmaR values sampled from a normal distribution with mean 0.36 and 0.4, respectively, and a coefficient of variation of 0.2 (Figure 5).

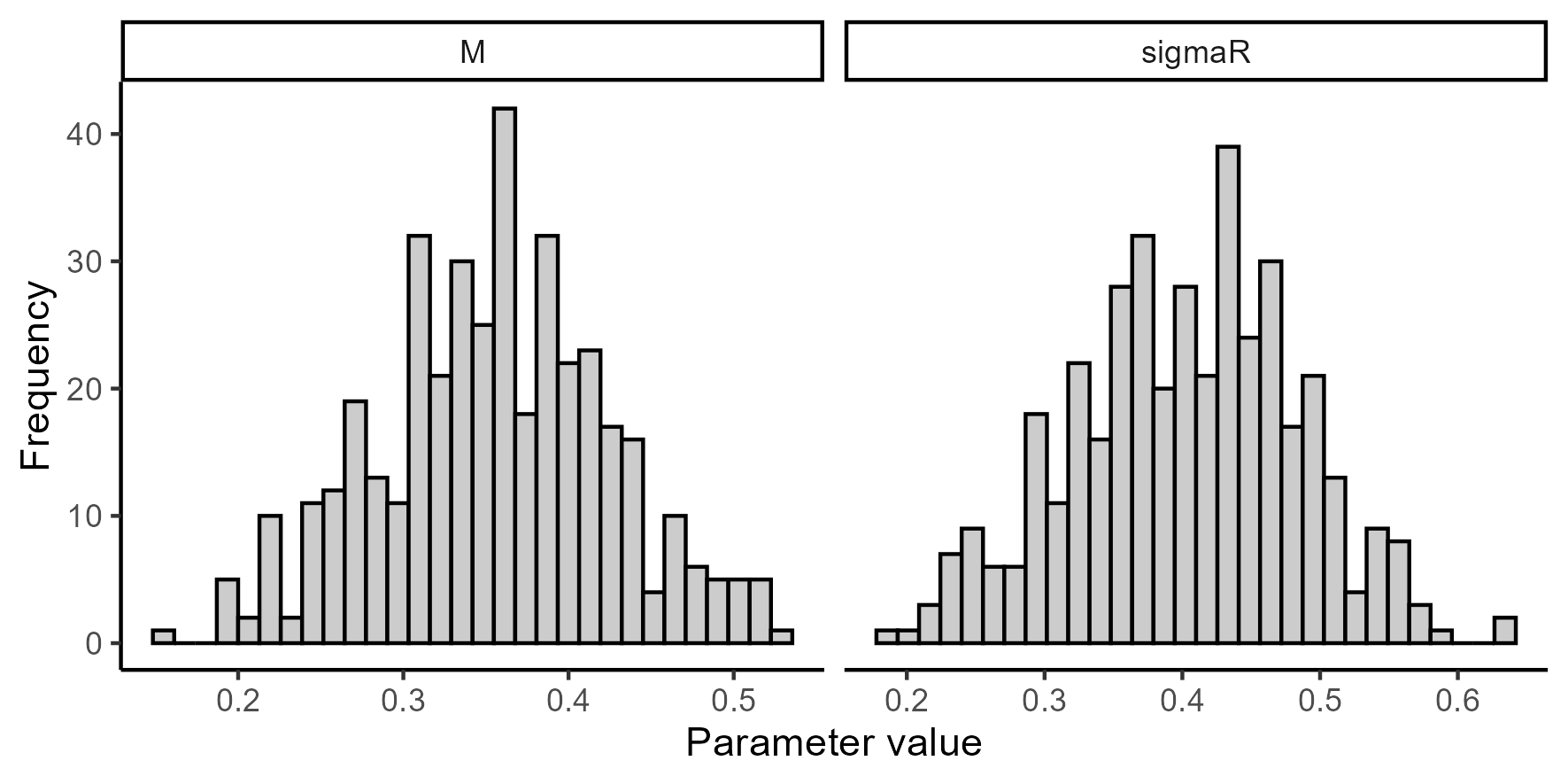
Figure 5: Values of natural mortality (M) and recruitment variability (sigmaR) simulated in the OMs.

Then, 100 models per weighting scenario were selected based on maximum gradient, likelihood, and the ratio of virgin and spawning biomass values in order to remove unrealistic or nonconvergent runs. We consider this final set of 400 models (100 models per weighting scenario) as our Reference OMs.

4.2 Robustness OMs

The robustness scenarios explored the impacts of changes in \(R_0\), recruitment variability, and maximum annual catch:

  • Changes in \(R_0\): decrease in the \(R_0\) parameter of the Beverton-Holt relationship by 20% in the simulation period from the estimated values in the Reference OMs.

  • Changes in sigmaR: increase in the recruitment variability by 20% in the simulation period from the estimated values in the Reference OMs.

  • Maximum catch (\(C_{max}\)): maximum annual catch of 100,000 tonnes.

4.3 Validation

4.3.1 Summary Report

A Summary Report summarizes the estimated parameters, the calculated biological reference points, and the estimated stock status relative to those reference points, across the 400 Reference OMs.

4.3.2 Diagnostic Reports

Individual diagnostic reports with objective function values and plots of model fits and patterns in residuals are available for each of the 400 Reference OMs. Table 2 presents the diagnostics for a subset of four OMs per weighting scenario with the most extreme M and sigmaR values.

Table 2: OM diagnostics reports. A set of four OMs were chosen per weighting scenario with the most extreme M and sigmaR values.
M sigmaR
BaseCase
Smallest M value 0.20 0.40 See diagnostics
Medium M value 0.36 0.26 See diagnostics
Largest M value 0.52 0.33 See diagnostics
Smallest sigmaR value 0.36 0.22 See diagnostics
Medium sigmaR value 0.36 0.40 See diagnostics
Largest sigmaR value 0.27 0.56 See diagnostics
CPUE
Smallest M value 0.15 0.24 See diagnostics
Medium M value 0.36 0.35 See diagnostics
Largest M value 0.53 0.49 See diagnostics
Smallest sigmaR value 0.34 0.18 See diagnostics
Medium sigmaR value 0.37 0.41 See diagnostics
Largest sigmaR value 0.43 0.63 See diagnostics
Size
Smallest M value 0.20 0.32 See diagnostics
Medium M value 0.36 0.27 See diagnostics
Largest M value 0.52 0.33 See diagnostics
Smallest sigmaR value 0.36 0.22 See diagnostics
Medium sigmaR value 0.40 0.40 See diagnostics
Largest sigmaR value 0.27 0.56 See diagnostics
Age
Smallest M value 0.22 0.35 See diagnostics
Medium M value 0.35 0.41 See diagnostics
Largest M value 0.50 0.47 See diagnostics
Smallest sigmaR value 0.36 0.20 See diagnostics
Medium sigmaR value 0.32 0.43 See diagnostics
Largest sigmaR value 0.43 0.63 See diagnostics

4.4 Conditioning

The Reference OMs were conditioned in FLBEIA with the same biological configuration and fleet structure of the SS3 models (Table 1). Two main periods are modelled in the MSE framework: historical and projection periods (Figure 6), with important differences in the data generation and observation error model (OEM).

timeline
    section 1930 - 2021
        Historical period : - Catches from observations <br> - CPUE from OEM
    section 2022 - 2050
        Simulation period : - Catches from HCR <br> - CPUE from OEM <br> - Evaluate MPs
Figure 6: Periods in the MSE and main differences between them.

4.4.1 Observation error model

Autocorrelation in CPUE residuals were introduced in the simulations based on a previous analysis of CPUE residuals in the stock assessment model (Table 3). This observation error was introduced both in the historical and projection period for all the Reference OMs.

Table 3: Evaluation of temporal autocorrelation in CPUE residuals for lag 1. \(\rho\) and \(\sigma\) represent the correlation parameter and the standard deviation of residuals, respectively. ACF is the autocorrelation function. The only fleet that assumed a \(\rho=0\) in the MSE was \(1_BB\).
Index ρ σ Sign. ACF? Autocorrelation
in MSE?		 Included in MSE
projection period?
1_BB 0.10 0.38 No No No
5_JPLL_N 0.25 0.30 No Yes Yes
6_JPLL_S 0.39 0.36 Yes Yes Yes
7_TAILL_N 0.13 0.29 No Yes Yes
8_TAILL_S 0.54 0.33 Yes Yes Yes
9_USLL_N 0.65 0.39 Yes Yes Yes
10_USLL_S 0.54 0.35 Yes Yes Yes
11_VENLL 0.57 0.42 Yes Yes No

5 Management Procedure

Simulated data was included in a stochastic surplus production model in continuous time (SPiCT). SPiCT is a full state-space model, where biomass and fishing dynamics are modelled as states, which are observed indirectly through biomass indices and commercial catches sampled with error (Pedersen and Berg, 2017). SPiCT calculates maximum sustainable yield (MSY) reference points and is able to make short-term projections. SPiCT is the estimation method in the MSE.

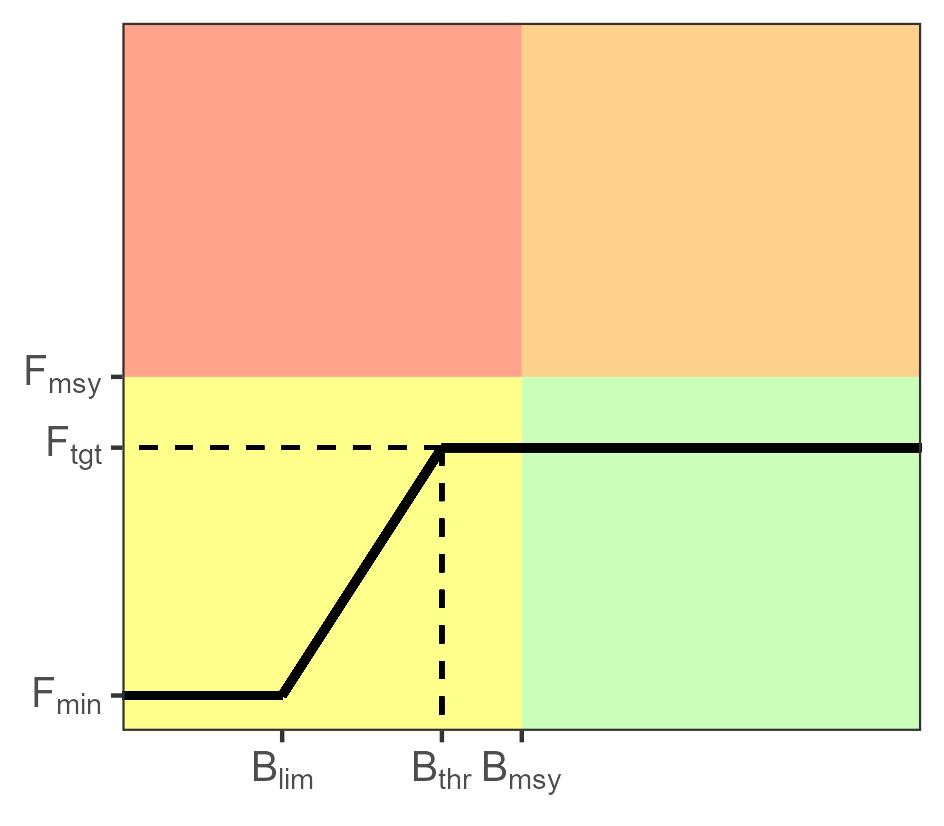
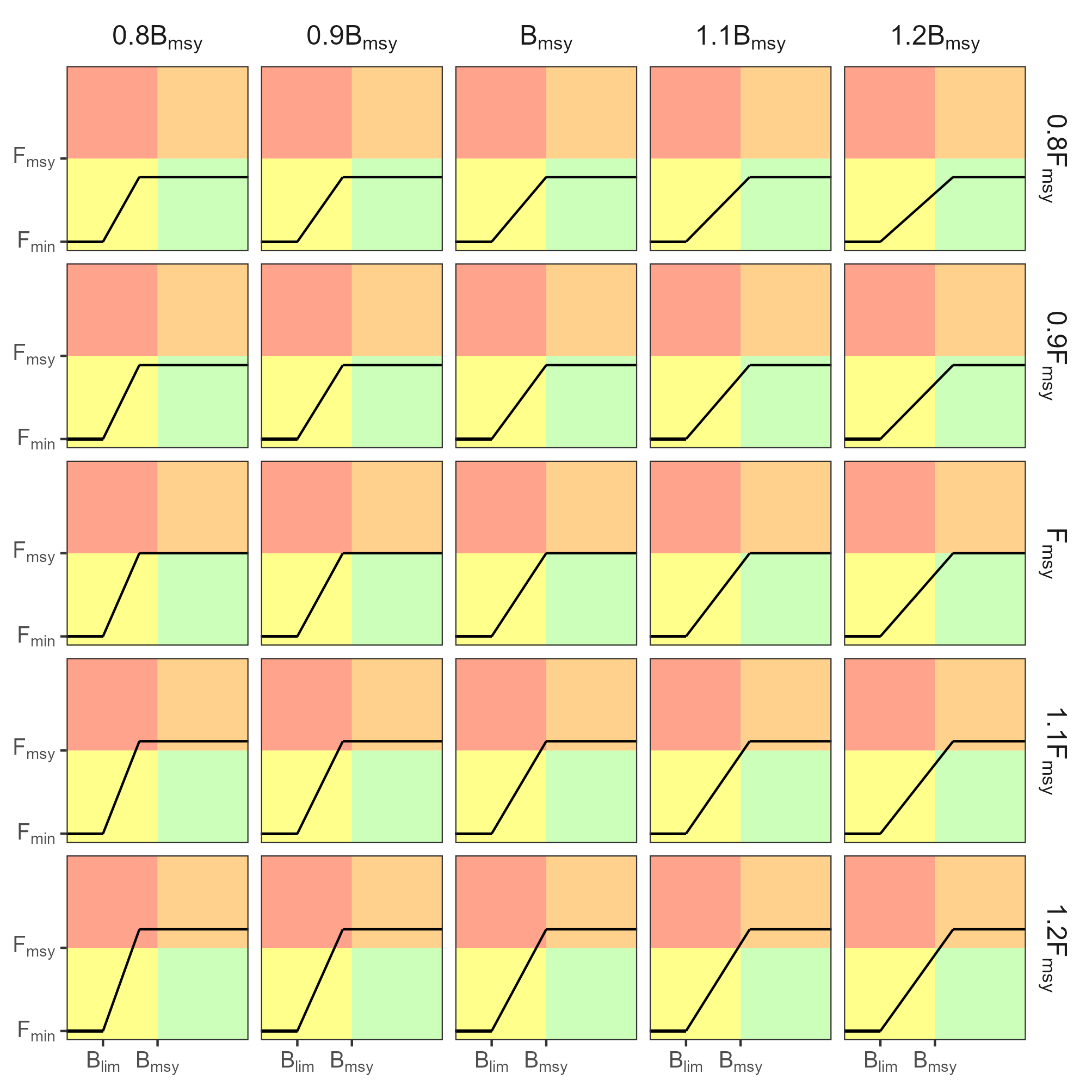
Figure 7: Example of harvest control rule (HCR).

The management advice is given every three years (management period) and the total allowable catch (TAC) is derived from a harvest control rule (HCR, Figure 7). We evaluated a total of 15 HCRs produced by the combinations of \(F_{tgt}\) and \(B_{thr}\) shown in Figure 8. \(B_{lim}=0.4\times B_{msy}\) and \(F_{mim}=0.1\times F_{msy}\) for all cases. In addition, we imposed the following restrictions:

  • The maximum TAC was 50,000 tonnes.
  • Maximum increase in catch from previous management period: 25%
  • Maximum decrease in catch from previous management period: 20%
Figure 8: HCR evaluated in the MSE. These HCR come from combinations of \(F_{tgt}\) (rows) and \(B_{thr}\) (columns).

6 Performance Metrics

25 PMs have been developed for the NALB MSE (Table 4) and are calculated in the simulation period. These PMs are grouped into four types:

  • Status: metrics related to stock status

  • Safety: metrics related to the probability of the stock not falling below the biological reference points

  • Yield: metrics related to the catch in the projection years

  • Stability: metrics related to the variation in the catches or TAC between management cycles

Each PM was calculated for every Reference OM (i.e., 400 PMs). Examples of each PM is given below.

Table 4: Performance metrics and description. These metrics were calculated from the simulation period.
Type Metric Symbol Description
Status Minimum spawner biomass relative to \(B_{msy}\) \(minB\) \(min(B_y/B_{msy})\)
Status Mean spawner biomass relative to \(B_{msy}\) \(meanB\) \((\prod_y B_y/B_{msy})^{1/n_y}\)
Status Mean fishing mortality relative to \(F_{msy}\) \(meanF\) \((\prod_y F_y/F_{msy})^{1/n_y}\)
Status Probability of being in the Kobe green quadrant \(pGreen\) Proportion of years in green quadrant (see Figure 7)
Status Probability of being in the Kobe red quadrant \(pRed\) Proportion of years in red quadrant (see Figure 7)
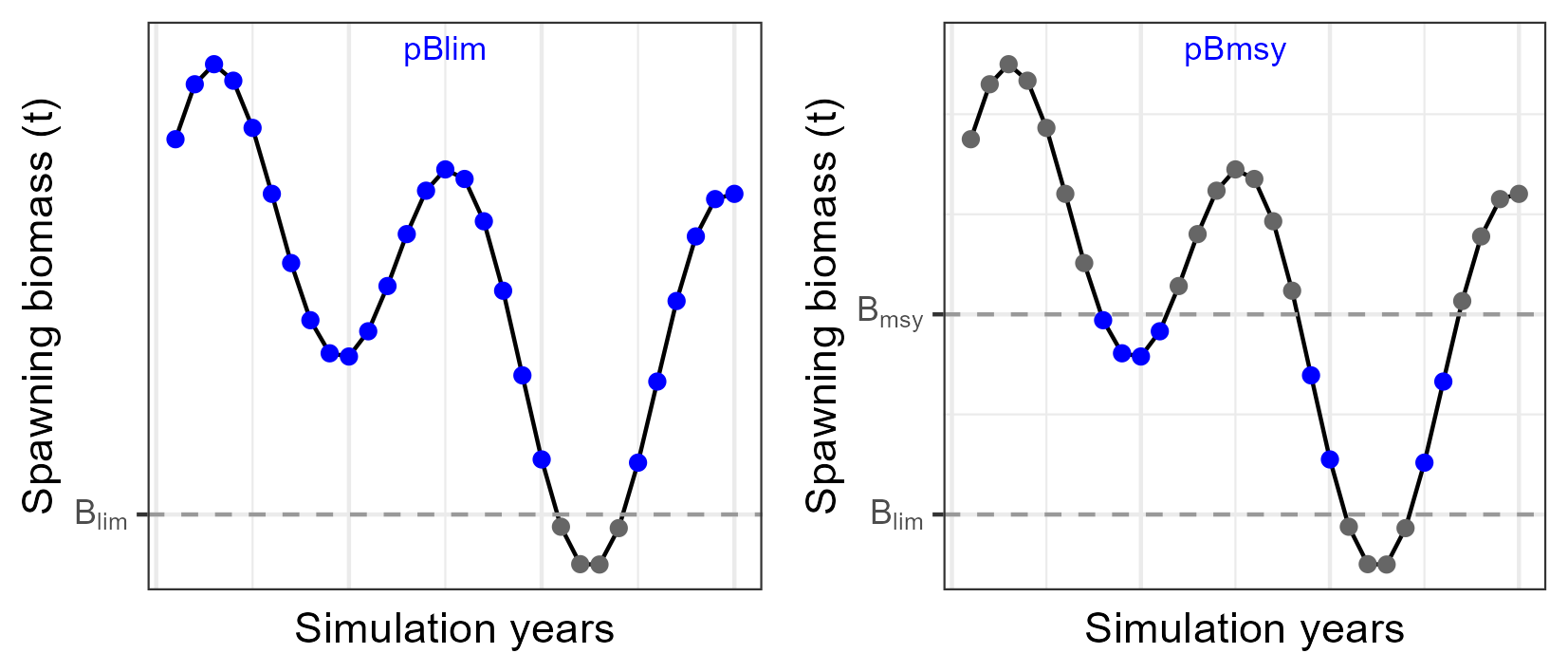
Safety Probability of \(B>B_{lim}\) \(pBlim\) Proportion of years that \(B>B_{lim}\)
Safety Probability of \(B_{lim}<B<B_{msy}\) \(pBmsy\) Proportion of years that \(B_{lim}<B<B_{msy}\)
Yield Mean catch (short term) \(Csht\) Mean catch from 1 to 3 years
Yield Mean catch (medium term) \(Cmed\) Mean catch from 5 to 10 years
Yield Mean catch (long term) \(Clon\) Mean catch from 15 to 25 years
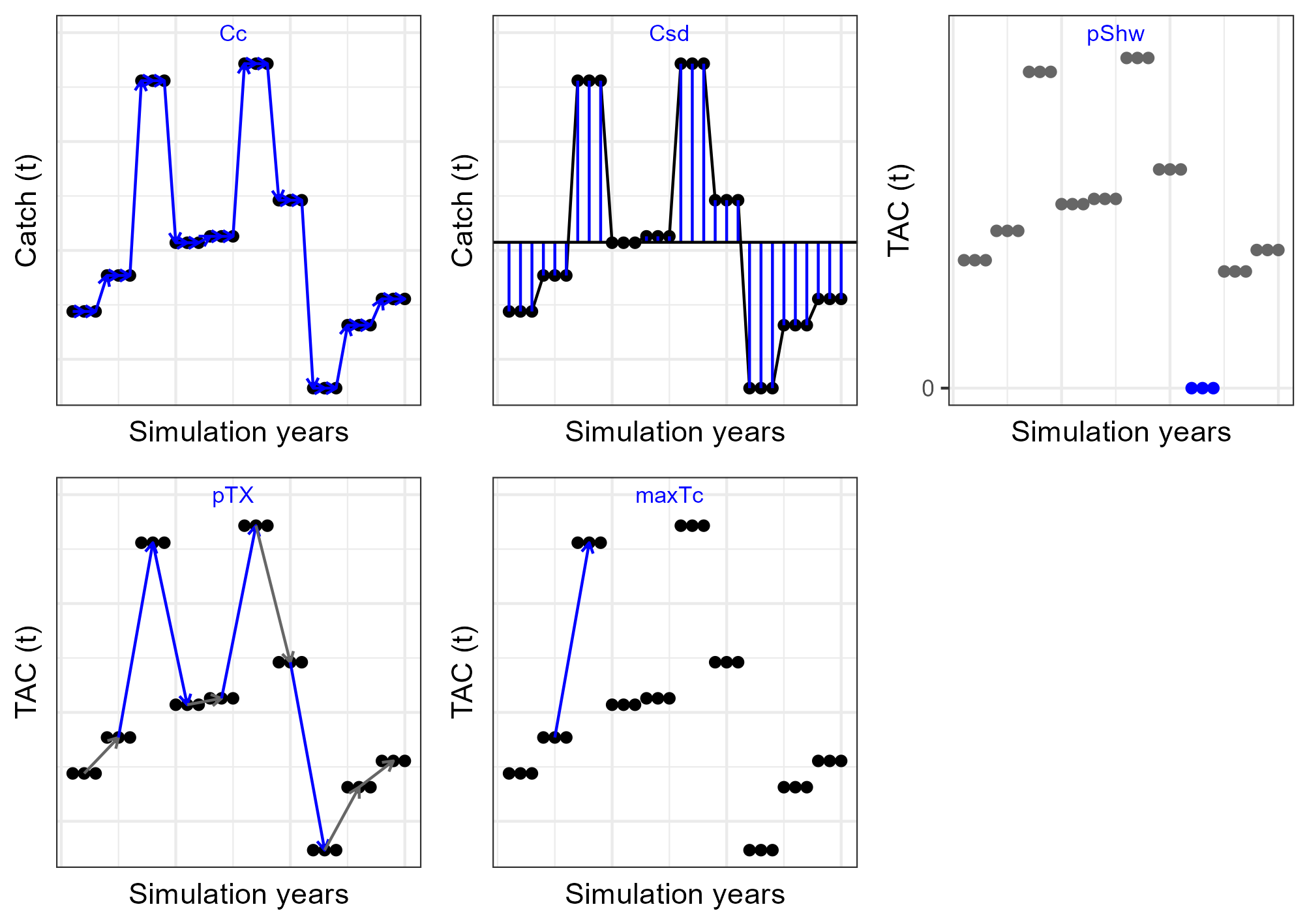
Stability Mean absolute proportional change in catch \(Cc\) Mean of \(\mid\frac{C_y - C_{y-1}}{C_{y-1}}\mid\)
Stability Standard deviation in catch \(Csd\) Catch standard deviation
Stability Probability of shutdown \(pShw\) Proportion of years that TAC=0
Stability Probability of TAC change over a certain level \(pTX\) Proportion of management cycles when the ratio of change \(\frac{TAC_y - TAC_{y-1}}{TAC_{y-1}} > 10\%\)
Stability Maximum amount of TAC change between management periods \(maxTc\) Maximum ratio of TAC change

6.1 Examples

6.1.1 Status

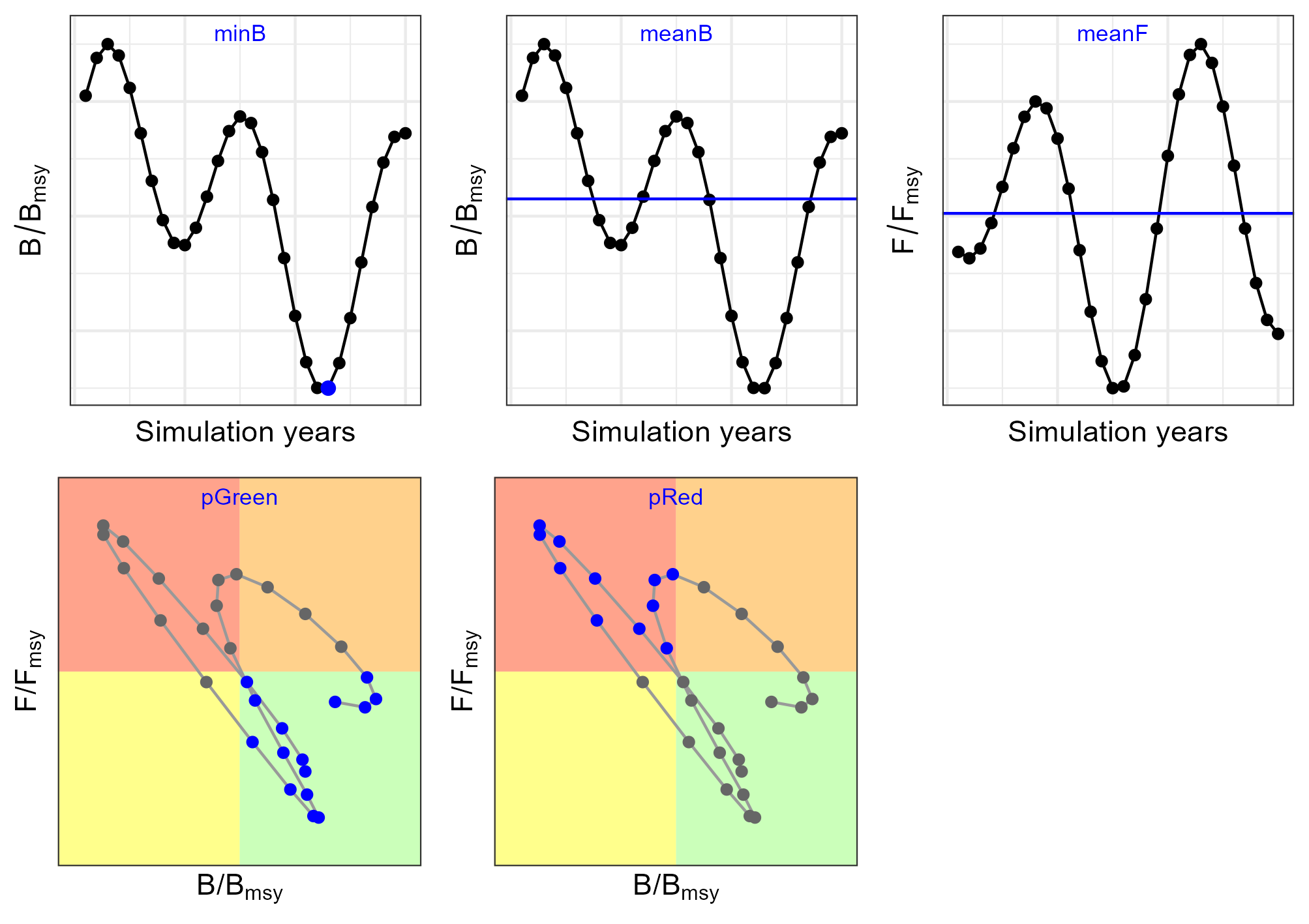
Figure 9: Status performance metrics. The blue dots or lines indicate the meaning of the metric. Find more details in Table 4.

6.1.2 Safety

Figure 10: Safety performance metrics. The blue dots indicate the meaning of the metric. Find more details in Table 4.

6.1.3 Yield

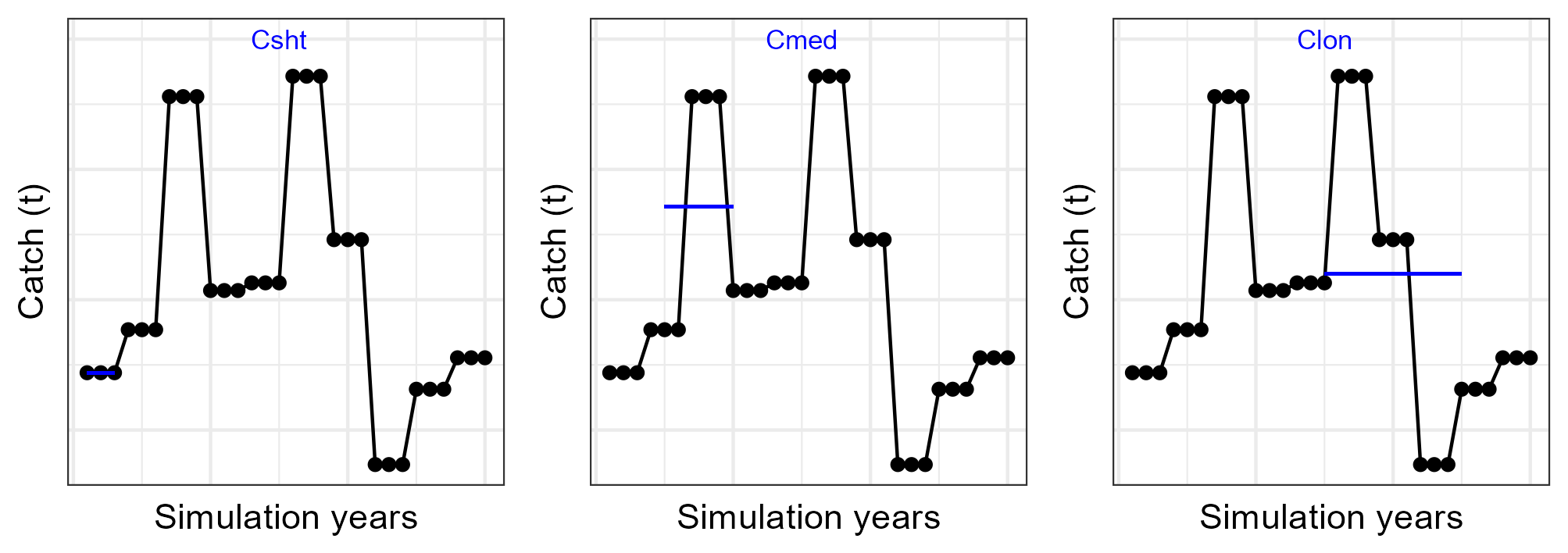
Figure 11: Yield performance metrics. The blue lines indicate the meaning of the metric. Find more details in Table 4.

6.1.4 Stability

Figure 12: Stability performance metrics. The blue lines, arrows, or dots indicate the meaning of the metric. Find more details in Table 4.

7 Results

7.1 Performance metrics

Table 5: Performance metrics results. Numbers indicate the median over the 400 PMs calculated per HCR and OM. The color scale is independent for every column.
Ftgt Bthr
Status
Safety
Yield
Stability
minB meanB meanF pGreen pRed pBlim pBmsy Csht Cmed Clon Cc Csd pShw pTX maxTc
0.8 0.8 1.45 1.60 0.74 100% 0% 100% 0% 50,000 43,507 38,233 −1% 4,960 0% 29% 17%
0.8 0.9 1.45 1.60 0.74 100% 0% 100% 0% 50,000 43,507 38,233 −1% 4,960 0% 29% 17%
0.8 1 1.45 1.60 0.74 100% 0% 100% 0% 50,000 43,507 38,250 −1% 4,983 0% 29% 17%
0.8 1.1 1.45 1.61 0.73 100% 0% 100% 0% 50,000 43,507 38,110 −1% 5,258 0% 43% 20%
0.8 1.2 1.46 1.62 0.71 100% 0% 100% 0% 50,000 43,421 37,467 −1% 5,871 0% 43% 20%
0.9 0.8 1.32 1.50 0.81 100% 0% 100% 0% 50,000 47,159 38,861 −1% 5,492 0% 29% 18%
0.9 0.9 1.32 1.51 0.80 100% 0% 100% 0% 50,000 47,159 38,819 −1% 5,492 0% 29% 19%
0.9 1 1.32 1.51 0.78 100% 0% 100% 0% 50,000 47,159 38,472 −1% 5,821 0% 43% 20%
0.9 1.1 1.32 1.52 0.77 100% 0% 100% 0% 50,000 47,116 37,683 −1% 6,517 0% 43% 20%
0.9 1.2 1.35 1.55 0.75 100% 0% 100% 0% 50,000 46,894 37,120 −1% 6,925 0% 57% 23%
1 0.8 1.22 1.43 0.86 88% 0% 100% 0% 50,000 49,090 39,787 −1% 5,397 0% 29% 19%
1 0.9 1.22 1.44 0.85 88% 0% 100% 0% 50,000 49,090 39,559 −1% 5,672 0% 29% 20%
1 1 1.22 1.45 0.84 88% 0% 100% 0% 50,000 49,090 38,276 −1% 6,647 0% 43% 20%
1 1.1 1.25 1.47 0.81 88% 0% 100% 0% 50,000 48,915 37,113 −1% 7,127 0% 43% 21%
1 1.2 1.28 1.51 0.78 96% 0% 100% 0% 50,000 48,333 37,054 −1% 7,255 0% 57% 24%
1.1 0.8 1.13 1.38 0.92 67% 0% 100% 0% 50,000 50,000 40,855 −1% 5,170 0% 29% 20%
1.1 0.9 1.14 1.40 0.90 67% 0% 100% 0% 50,000 50,000 39,902 −1% 5,896 0% 29% 20%
1.1 1 1.15 1.41 0.87 75% 0% 100% 0% 50,000 50,000 38,527 −1% 6,795 0% 43% 20%
1.1 1.1 1.19 1.44 0.83 81% 0% 100% 0% 50,000 49,939 37,055 −1% 7,122 0% 43% 20%
1.1 1.2 1.25 1.47 0.81 88% 0% 100% 0% 50,000 48,959 37,122 −1% 7,248 0% 43% 22%
1.2 0.8 1.06 1.34 0.96 54% 0% 100% 0% 50,000 50,000 42,213 −1% 4,820 0% 29% 20%
1.2 0.9 1.07 1.36 0.92 58% 0% 100% 0% 50,000 50,000 41,046 −1% 6,003 0% 29% 20%
1.2 1 1.11 1.38 0.89 67% 0% 100% 0% 50,000 50,000 39,263 −1% 6,644 0% 43% 20%
1.2 1.1 1.15 1.42 0.86 75% 0% 100% 0% 50,000 50,000 38,069 −1% 6,938 0% 43% 20%
1.2 1.2 1.21 1.45 0.82 83% 0% 100% 0% 50,000 49,665 37,086 −1% 7,234 0% 43% 21%
Table 6: Performance metrics results for robustness scenarios. Numbers indicate the median over the 400 PMs calculated per HCR and OM. The color scale is independent for every column.
Scen Ftgt Bthr
Status
Safety
Yield
Stability
minB meanB meanF pGreen pRed pBlim pBmsy Csht Cmed Clon Cc Csd pShw pTX maxTc
Cmax 0.8 1 1.42 1.57 0.75 100% 0% 100% 0% 53,222 42,862 37,933 −1% 6,729 0% 43% 20%
Cmax 1 1 1.11 1.37 0.88 58% 0% 100% 0% 59,064 50,817 35,175 −1% 10,696 0% 71% 25%
Cmax 1.2 1 0.84 1.13 1.04 33% 31% 100% 21% 59,064 60,273 30,696 −2% 14,890 0% 86% 25%
R0 0.8 1 0.91 1.18 0.78 50% 4% 100% 29% 50,000 42,000 22,821 −3% 10,890 0% 71% 20%
R0 1 1 0.69 0.99 0.94 21% 33% 100% 54% 50,000 48,333 21,939 −4% 13,164 0% 71% 20%
R0 1.2 1 0.60 0.91 1.06 17% 42% 100% 54% 50,000 48,333 21,939 −4% 13,281 0% 71% 20%
sigma 0.8 1 1.24 1.80 0.70 100% 0% 100% 0% 50,000 44,403 41,431 −0% 4,666 0% 29% 20%
sigma 1 1 1.14 1.68 0.77 92% 0% 100% 0% 50,000 49,559 45,982 −0% 4,046 0% 29% 20%
sigma 1.2 1 1.03 1.60 0.82 75% 0% 100% 0% 50,000 50,000 47,000 −0% 3,378 0% 21% 20%
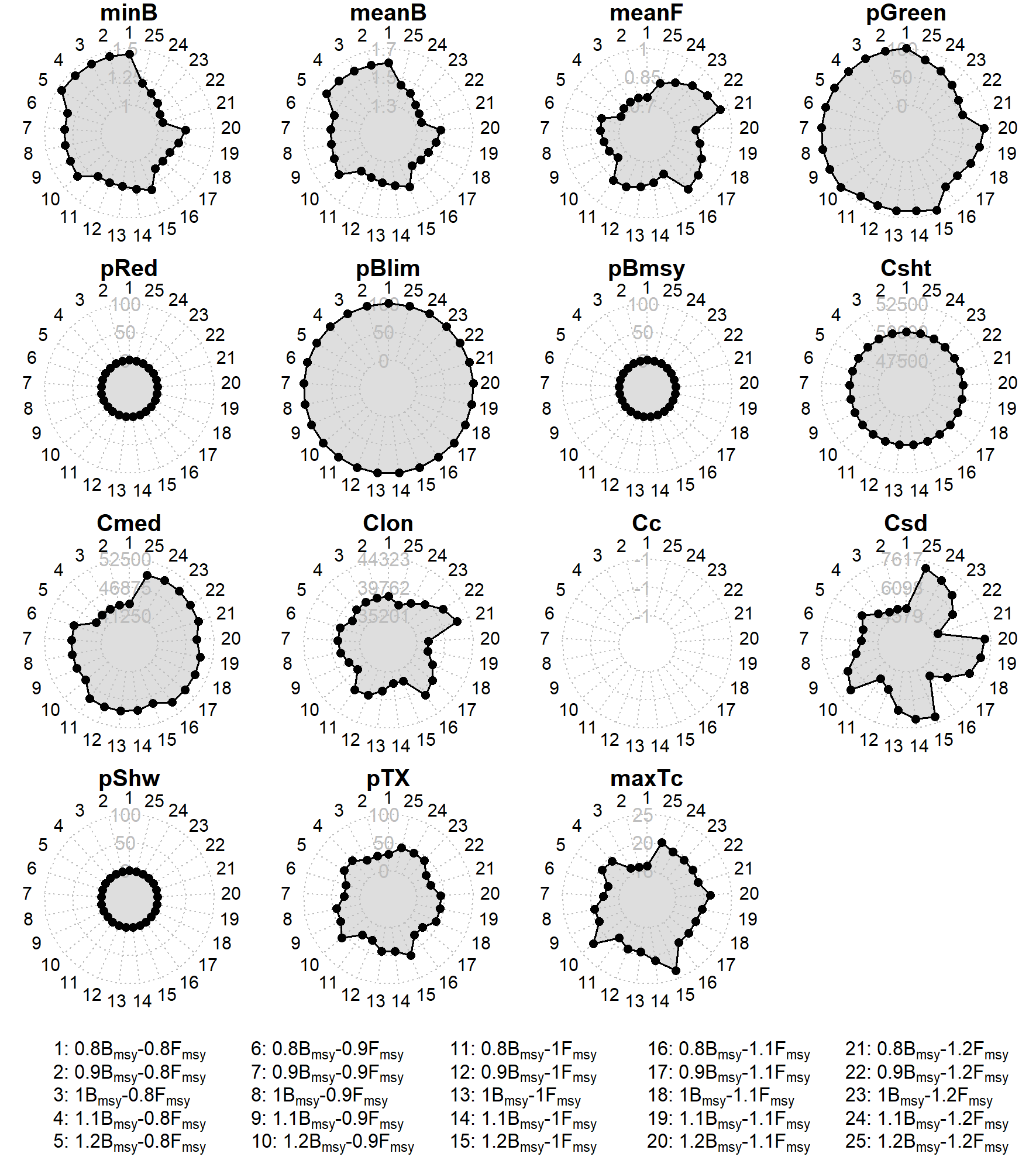
Figure 13: Performance metrics for main scenarios.

8 Glossary

Term Definition
NALB North Atlantic Albacore
OM Operating model
CMP Candidate management procedure
PM Performance metric
ALBSG Albacore Species Group
SS3 Stock Synthesis 3 platform
ESS Effective sample size
CAAL Conditional age-at-length
M Natural mortality
sigmaR Variability in recruitment
h Steepness in the stock-recruit function
OEM Observation error model
HCR Harvest control rule
TAC Total Allowable Catch

References

Fournier, D.A., Hampton, J., Sibert, J.R., 1998. MULTIFAN-CL: A length-based, age-structured model for fisheries stock assessment, with application to South Pacific albacore, Thunnus Alalunga. Canadian Journal of Fisheries and Aquatic Sciences 55, 2105–2116. https://doi.org/10.1139/f98-100
Francis, R.I.C.C., 2011. Data weighting in statistical fisheries stock assessment models. Canadian Journal of Fisheries and Aquatic Sciences 68, 1124–1138. https://doi.org/10.1139/f2011-025
Garcia, D., Sánchez, S., Prellezo, R., Urtizberea, A., Andrés, M., 2017. FLBEIA: A simulation model to conduct Bio-Economic evaluation of fisheries management strategies. SoftwareX 6, 141–147. https://doi.org/10.1016/j.softx.2017.06.001
Hamel, O.S., Cope, J.M., 2022. Development and considerations for application of a longevity-based prior for the natural mortality rate. Fisheries Research 256, 106477. https://doi.org/10.1016/j.fishres.2022.106477
ICCAT, 2023. Report of the 2023 ICCAT Atlantic albacore stock assessment meeting (including MSE) (No. SCRS/2023/010). ICCAT (International Commission for the Conservation of Atlantic Tunas).
Lorenzen, K., 1996. The relationship between body weight and natural mortality in juvenile and adult fish: A comparison of natural ecosystems and aquaculture. Journal of Fish Biology 49, 627–642. https://doi.org/10.1111/j.1095-8649.1996.tb00060.x
Merino, G., De Bruyn, P., Scott, G.P., Kell, L., Arrizabalaga, H., 2014. A preliminary stock assessment for northern albacore using the fully integrated stock assessment model, MULTIFAN-CL (No. SCRS/2013/058). ICCAT (International Commission for the Conservation of Atlantic Tunas).
Merino, G., Kell, L., Arrizabalaga, H., Santiago, J., 2020. Updated consolidated report for North Atlantic albacore management strategy evaluation (No. SCRS/2020/153). ICCAT (International Commission for the Conservation of Atlantic Tunas).
Methot, R.D., Wetzel, C.R., 2013. Stock synthesis: A biological and statistical framework for fish stock assessment and fishery management. Fisheries Research 142, 86–99. https://doi.org/10.1016/j.fishres.2012.10.012
Pedersen, M.W., Berg, C.W., 2017. A stochastic surplus production model in continuous time. Fish and Fisheries 18, 226–243. https://doi.org/10.1111/faf.12174
Schnute, J., 1981. A versatile growth model with statistically stable parameters. Canadian Journal of Fisheries and Aquatic Sciences 38, 1128–1140. https://doi.org/10.1139/f81-153